Soustavy lineární a kvadratické rovnice
Tyto soustavy se nejčastěji řeší dosazovací metodou. Z lineární rovnice si vyjádříme jednu neznámou, a toto vyjádření dosadíme do rovnice kvadratické. Pokud získaná kvadratická rovnice bude mít dva kořeny, nesmíme zapomenout k oběma dopočítat hodnotu druhé neznámé. ![]() Nebude-li kvadratická rce mít ani jeden kořen, nemá celá soustava řešení.
Nebude-li kvadratická rce mít ani jeden kořen, nemá celá soustava řešení.
-
Příklad 1
Řešte v
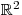 soustavu rovnic.
soustavu rovnic.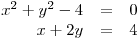
-
Řešení
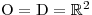 .
.Z první rovnice si vyjádříme neznámou x:
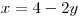
Toto vyjádření dosadíme do druhé, kvadratické, rovnice, kterou vyřešíme:
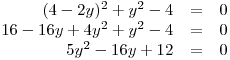
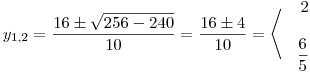
Pro obě hodnoty y dopočítáme x:
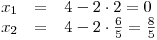
Pak už jen zapíšeme K.
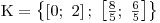
 Zápis množiny K je možná trošku komplikovanější, ale je jím potřeba vyjádřit,
Zápis množiny K je možná trošku komplikovanější, ale je jím potřeba vyjádřit,
že množina všech řešení soustavy obsahuje dvě uspořádané dvojice kořenů.

Soustavy dvou kvadratických rovnic
Pro řešení soustavy dvou kvadratických rovnic se už nedá napsat univerzální postup řešení. Vše záleží na složitosti zadání, protože někdy nám stačí k vyřešení soustavy sčítací metoda. Jindy, pokud je alespoň v jedné rovnici jedna neznámá pouze v první mocnině, můžeme jí z této rovnice vyjádřit a použít metodu dosazovací. V dalších případech je řešení záležitostí různých triků a nápadů řešitele.
Ukážeme si alespoň první dvě varianty.
-
Příklad 2
Řešte v
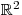 soustavu rovnic:
soustavu rovnic: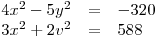
-
Řešení
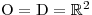
Tentokrát použijeme sčítací metodu. Předtím je ale potřeba soustavu trochu upravit.
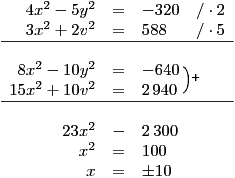
Pro každou získanou hodnotu x dopočteme y dosazením do první rovnice v zadání.
Pro x1 = 10:
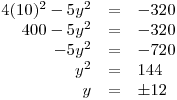
Měli bychom poznat, že stejný výpočet bychom prováděli i pro x1 = −10 a získali bychom stejné hodnoty y:
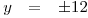
Teď už můžeme zapsat K. Pozor, tentokrát rovnici řeší 4 uspořádané dvojice!
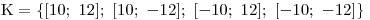
 Tuto rovnici bychom mohli řešit i dosazovací metodou,
Tuto rovnici bychom mohli řešit i dosazovací metodou,
jen bychom si nevyjadřovali z nějaké rce x, ale x2.

-
Příklad 3
Řešte v
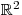 soustavu rovnic:
soustavu rovnic: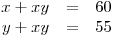
-
Řešení
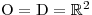
Tuto rovnici budeme řešit dosazovací metodou. Vyjádříme si z první rovnice x:
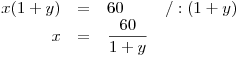
Při tomto vyjadřování x jsme ale prováděli neekvivalentní úpravu. Dělili jsme obě strany rovnice výrazem, který by mohl být nulový. Můžeme tedy další postup provádět jen pro y ≠ −1. Tím bychom ale mohli přijít o nějaké řešení, a tak si raději v zadání ověříme, že pro y = −1 neexistuje takové x, aby tato dvojice řešila soustavu:
Dosadíme y = −1 do druhé rovnice a vypočteme, že x = −56. Naštěstí ale dvojice [−56; −1] první rovnici v soustavě neřeší, a tak můžeme pokračovat dál v dosazovací metodě s tím, že jsme o žádné řešení nepřišli.
Nyní vyjádření x dosadíme do druhé rovnice:
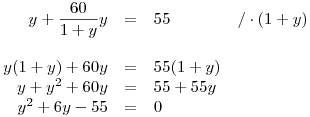
Vypočteme y:
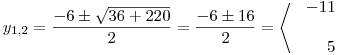
Zpětným dosazením do vyjádření x z první rovnice vypočítáme také x.
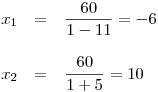
Na závěr zapíšeme
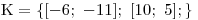 .
. Stále je nutné doržovat ekvivalentnost úprav všech rovnic, jinak bychom mohli přicházet
Stále je nutné doržovat ekvivalentnost úprav všech rovnic, jinak bychom mohli přicházet
o řešení, nebo si přidávat nová. Pokud kvůli nějaké úpravě jsme nuceni nějaké hodnoty
neznámých zakázat, je dobré si ověřit, že to zrovna nejsou řešení, která hledáme.
