Řešení soustav tří rovnic s třemi neznámými
Stejně jako u řešení soustav dvou rovnic s dvěma neznámými, musíme u příkladů se třemi neznámými rozšířit obor řešení O. Soustavy budeme tedy standardně řešit v 
(častěji se užívá zkrácený zápis 
) a řešením budou uspořádané trojice.
Použití sčítací a dosazovací metody
Obě metody, se kterými jsem se seznámili v předchozí kapitole, se dají použít i pro řešení soustav tří lineárních rovnic s třemi neznámými. V praxi se ale moc nepoužívají, protože jsou poměrně zdlouhavé. Jejich použitím se soustava tří rovnic se třemi neznámými převede na soustavu dvou rovnic o dvou neznámých, kterou pak řešíme nějakou z těchto dvou metod, a získané dva kořeny pak dosadíme do libovolné rovnice v zadání a dopočte třetí.
Sčítací metoda
Použití sčítací metody spočívá ve vhodném sečtení dvou různých dvojic rovnic tak, abychom z těchto dvou součtů získali dvě rovnice jen s dvěma neznámými.
-
Ukázka 1
-
Začneme-li řešit soustavu rovnic
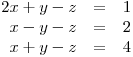
sčítací metodou, můžeme sečíst první rovnici se druhou a druhou rovnici se třetí. Tímto součtem získáme soustavu dvou rovnic s neznámými x a z, protože y se navzájem vyruší:
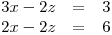
A tuto soustavu už umíme vyřešit třeba sčítací, nebo dosazovací metodou…
Dosazovací metoda
Řešení soustavy dosazovací metodou spočívá ve vyjádření libovolné neznámé z jedné rovnice a následném dosazení tohoto vyjádření za onu neznámou do zbylých dvou rovnic. Tím z těchto dvou rovnic uděláme soustavu dvou rovnic pro dvě neznámé.
-
Ukázka 2
-
Začneme-li opět řešit soustavu rovnic
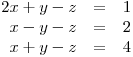
tentokrát dosazovací metodou, vyjádříme si třeba z druhé rovnice neznámou x:
a toto vyjádření dosadíme za x do první i třetí ro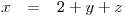vnice
Nikdy nesmíme dosadit zpět do té rovnice,
ze které jsme tu neznámou vyjadřovali. a dostaneme soustavu 2 rovnic s dvěma neznámými: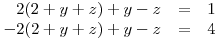
Tu zase můžeme dále řešit sčítací, nebo dosazovací metodou…
Srovnávací (komparační) metoda
Srovnávací metoda je podobná dosazovací metodě. Ze všech tří rovnic si vyjádříme jednu a tu samou neznámou. Tato vyjádření mezi sebou vhodně porovnáváme. Vše podrobněji ukážeme na příkladu.
-
Příklad 1
Řešte v
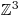soustavu rovnic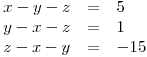
-
Řešení
Nejprve určíme O = D =
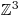.Z každé rovnice vyjádříme třeba neznámou x:
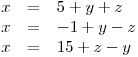
Z těchto tří vyjádření nyní sestavíme dvě rovnice. Vezmeme třeba vyjádření x z první a druhé rovnice, které porovnáme mezi sebou. Totéž určíme z první a třetí rovnice. Dostaneme soustavu dvou rovnic pro dvě neznámé, které rovnou upravíme
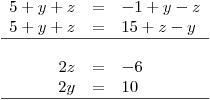
Náhodou se nám podařilo sestavit takové rovnice, že nám obě poskytly rovnou hodnoty pro yi z. Alespoň teď nemusíme řešit soustavu sčítací, nebo dosazovací metodou.
Dopočteme tedy ještě x, dosazením do vyjádření x z první rovnice.
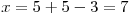
Pak už jen zapíšeme K, jako množinu obsahující uspořádanou trojici:
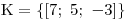
Početně nenáročný příklad, ale pozor na správné zápisy všech postupů. Také je důležité
nezapomenout vypočítat kořeny pro obě neznámé, ne jen pro jednu.
Gaussova eliminační metoda
Tato metoda je jedna z nejvhodnějších pro řešení soustav více rovnic o více neznámých. Někdy má samozřejmě soustava tvar, že je výhodnější použít některou z výše uvedených metod, ale pokud byste se chtěli naučit jen jednu univerzální metodu, je Gaussova eliminace to pravé. Navíc oproti jiným metodám má výhodu, že se dá velmi efektivně použít i na soustavy více rovnic než tří, což pro ostatní metody už neplatí. Metoda je pojmenována po Carlu Friedrichu Gaussovi, významném německém matematikovi.
Tato metoda spočívá v úpravě dané soustavy na tzv. trojúhelníkový tvar, který vypadá pro soustavu tří rovnic takto:
|
 |
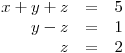Máme-li totiž soustavu upravenou do trojúhelníkového tvaru, není již problém dopočítat kořeny pro jednotlivé neznámé. Z poslední rovnice získáme hodnotu poslední neznámé, tu dosadíme do druhé rovnice a vypočteme hodnotu druhé neznámé a obě hodnoty pak dosadíme do první rovnice a dopočítáme poslední neznámou.
Postup Gaussovy eliminační metody
- Rovnice uspořádáme tak, aby v první rovnici u první neznámé byl nenulový koeficient. Výhodné ještě bývá tuto rovnici upravit (buď ekvivalentními úpravami,
nebo přičtením násobku libovolné jiné rovnice) tak, aby koeficient u první neznámé byl 1. - K 2. a 3. rovnici přičteme takový násobek první rovnice, abychom v jejich součtu eliminovali členy s první neznámou.
- Druhou a třetí rovnici uspořádáme tak, aby druhá rovnice měla nenulový koeficient u druhé neznámé.Opět je výhodné druhou rovnici upravit tak, aby koeficient u 2. neznámé byl 1.
- K 3. rovnici přičteme takový násobek druhé rovnice, abychom v jejich součtu eliminovali členy s druhou neznámou.
Tento postup jen efektivně využívá ekvivalentní úpravy soustavy rovnic, proto jej nebudeme více rozebírat a rovnou si jej ukážeme v praxi.
-
Příklad 2
Řešte v
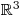soustavu rovnic: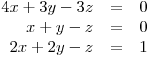
-
Řešení
Nejprve určíme O = D =
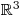.Jako první krok zpřeházíme rovnice tak, aby u x v první rovnici byla jednička. To splňuje druhá rovnice a tak ji prohodíme s první rovnicí.
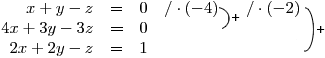
Na místo druhé rovnice pak napíšeme mínus čtyřnásobek první rovnice sečtený s druhou rovnicí. Místo třetí rovnice napíšeme sečtený mínus dvojnásobek první rovnice s třetí.
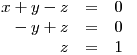
Máme soustavu upravenou do trojúhelníkového tvaru a zbývá už jen dopočítat hodnoty pro jednotlivé neznámé.
Z poslední rovnice snadno určíme, že
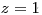. Tuto hodnotu pak dosadíme do druhé rovnice a dopočítáme y a pak pomocí první rovnice i x.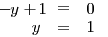
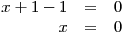
Soustava má právě jedno řešení, uspořádanou trojici [0; 1; 1], a tak můžeme zapsat K.
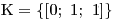
Vhodným prohazováním rovnic (někdy je též dovoleno měnit pořadí neznámých) si můžeme
výrazně usnadnit počítání, protože na klíčová místa umisťujeme výrazy s koeficinetem 1.
Gaussova eliminační metoda, stejně jako srovnávací metoda, se dá samozřejmě použít i pro soustavy dvou rovnic pro dvě neznámé. Ale tam většinou použití sčítací, nebo dosazovací metody vede k výsledku rychleji.