Pojem kvadratické nerovnice
- Kvadratickou nerovnicí
-
s neznámou x nazveme každou nerovnici, kterou je možné ekvivalentními úpravami převést na jeden z těchto tvarů:
ax2 + bx +c > 0 ax2 + bx +c < 0 ax2 + bx +c ≥ 0 ax2 + bx +c ≤ 0, kde koeficienty a, b, c ∈
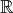a a ≠ 0.Tyto čtyři tvary kvadratických nerovnic pro potřeby této kapitoly nazveme základními tvary kvadratické nerovnice.
Řešení obecných kvadratických nerovnic je obtížnější než řešení kvadratických rovnic. Ukážeme si dvě metody. První z nich je pro začátečníky jednodušší na pochopení, ale je vcelku pracná, a bohužel se nedá použít pro všechny typy kvadratických nerovnic. Druhá metoda je oproti tomu složitější, ale pokud se ji naučíme, řešení kvadratických nerovnic touto metodou bude rychlé a krátké. Tuto druhou metodu lze použít pro jakoukoliv kvadratickou nerovnici.
Řešení pomocí rozkladu na součin
Tato metoda je velmi jednoduchá, ale potřebujeme pro ni znát řešení kvadratických rovnic, rozložení kvadratického trojčlenu na součin a také vědět, jak se řeší nerovnice v součinovém tvaru.
Z kvadratické nerovnice v jednom ze základních tvarů vezmeme kvadratický trojčlen ax2 + bx +c , který pomocí Vietových vzorců rozložíme na součin lineárních dvojčlenů a(x − x1)(x − x2). To lze udělat pouze za podmínky, že diskriminant D příslušné kvadratické rovnice ax2 + bx +c = 0 je nezáporný.
Pokud D < 0, pak tuto metodu nelze použít, pokud O = !
Tím jsme danou nerovnici ve tvaru např. ax2 + bx +c ≥ 0 převedli na nerovnici v součinovém tvaru
a(x − x1)(x − x2) ≥ 0, kterou už umíme řešit. Stačí určit nulové body jednotlivých lineárních dvojčlenů, sestavit tabulku a pomocí variace znamének dvojčlenů a koeficientu a určit, pro která x je daný součin kladný nebo nulový.
Řešené příklady
-
Příklad 1
Řešte v
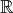nerovnici 
. -
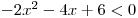Řešení
Nejprve určíme, že
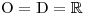.Abychom mohli kvadratický trojčlen rozložit na součin lineárních dvojčlenů, potřebujeme vypočítat kořeny příslušné kvadratické rovnice
.
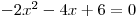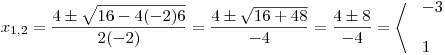
Nerovnici
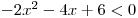pak můžeme přepsat jako 
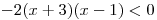.Nulové body lineárních dvojčlenů v závorkách už máme určeny, protože to jsou čísla x1 a x2. Sestavíme proto tabulku a vyčteme z ní řešení této nerovnice.
(− 
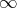; −3)− 3 (− 3 ; 1) 1 (1 ; 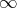)− 2 
Do jednoho z řádků tabulky je vhodné uvést i činitel− 2, protože i ten nám bude
ovlivňovat výsledné znaménko součinu na levé straně nerovnosti. Jeho znaménko je
stále záporné, nezávislé na hodnotě x.− − − − − x + 3 − 0 + + + x − 3 − − − 0 +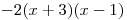 
− 0 + 0 − Hledáme intervaly, ve kterých je součin v nerovnici menší než nula. Vyhovují nám tedy intervaly, kde nám výsledný součin vyšel záporný, viz žlutě vyznačené sloupce.
Ještě zapíšeme
.
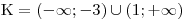Jednoduché převedení kvadratické nerce na nerci v součinovém tvaru nám umožnilo
spolehlivě vyřešit zadaný příklad. V tabulce je pak důležité mít obsaženy všechny činitele, které
ovlivní výsledné znaménko celé levé strany nerce.
Ve druhém příkladu si ukážeme použití této metody v případě, že příslušná kvadratická rovnice k zadané nerovnici má diskriminant nulový a vyjde jen jeden, dvojnásobný, kořen.
-
Příklad 2
Řešte v
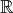nerovnici 
. -
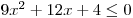Řešení
Nejprve opět určíme, že
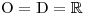.Vypočteme kořeny příslušné kvadratické rovnice
.
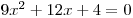Zadanou kvadratickou nerovnici
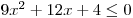tedy můžeme přepsat jako 
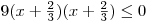. Chceme-li kvadratický trojčlen přepsat jako součin v případě, když
diskriminant příslušné rce je nulový, musíme vypočtený kořen použít
dvakrát. Proto se tento kořen někdy nazývá dvojnásobný.Nyní opět můžeme použít tabulku s nulovými body (
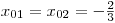), nebo můžeme provést následující úvahu:Díky stejným lineárním dvojčlenům v závorkách, můžeme nerovnici upravit na tvar
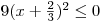. Podíváme-li se na nerovnici jako na podmínku pro vztah dvou výrazů, chceme, aby součin devítky a výrazu 
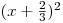byl záporný, nebo nulový.Číslo devět je kladné, museli bychom ho vynásobit něčím záporným, nebo nulovým, abychom dostali záporný, nebo nulový výsledek. Výraz
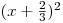je ale díky druhé mocnině vždy nezáporný. Nikdy nebude záporný, ale pro 
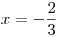bude nulový.Tedy výraz na levé straně nerovnosti nebude nikdy záporný, ale pro
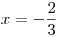bude výraz nulový, což nám pro splnění požadované nerovnosti stačí.Množina všech kořenů K bude obsahovat pouze tuto jednu hodnotu, neboli
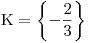. Zapsané úvahy v postupu jsou možná pro někoho složité, ale pokud je pochopíte a provedete,
můžete si usnadnit řešení tohoto příkladu. Jinak je možné samozřejmě použít řešení pomocí
tabulky, nebo pomocí dvou soustav lineárních nerovnic.
Řešení dosazením při záporném diskriminantu
Někdy se stane, že při řešení příslušné kvadratické rovnice k dané nerovnici vyjde diskriminant záporný. Podle dříve uvedeného to znamená, že kvadratický trojčlen v základním tvaru nerovnice nepůjde rozložit na součin. Nemůžeme proto použít metodu řešení kvadratické nerovnice jako nerovnice v součinovém tvaru.
Pro řešení takové nerovnice v tomto případě existují jen dvě možnosti:
- nerovnice nemá žádné kořeny
- nerovnici řeší všechna čísla z definičního oboru D
V tomto se zase rce liší od nerce. U rce záporný diskriminant automaticky signalizuje prázdnou množinukořenů, u nerce to může být prázdná množina, ale stejně pravděpodobná je i možnost nekonečně mnoho
kořenů. Je tedy nutné vždy odlišovat zda řešíme rci, nebo nerci!
Tu správnou poznáme pomocí jednoduchého dosazení. Zvolíme libovolné číslo z D , které do nerovnice dosadíme za x. Pokud nám po dosazení a upravení levé i pravé strany vyjde pravdivá nerovnost, pak nerovnici řeší každé číslo z D. Pokud dostaneme nerovnost nepravdivou, pak daná nerovnice nemá žádné řešení v daném O.