ROVNICE
A NEROVNICE

Úvod Lineární rovnice Lineární nerovnice  Test 1 – lineární Kvadratické rovnice Kvadratické nerovnice  Test 2 – kvadratické Iracionální rce a nerce Parametry a abs. hodn. Rce a nerce s abs. hodn. Rce s parametry Nerce s parametry Úlohy Rovnice vyšších řádů  Test 3 Soustavy rovnic  Test 4 – soustavy Odkazy a literatura
Přehled stránek

Pojem absolutní hodnoty

Absolutní hodnota

reálného čísla a (značíme |a|) je definována:

|a| = a, pro a nezáporná,

|a| = −a pro a záporná. Tento symbolický zápis vlastně znamená, že abs. hodnota s nezápornými
čísly nic nedělá a ze záporných čísel dělá čísla opačná (neboli u záporných
čísel zruší jejich záporné znaménko).

Pro libovolná reálná čísla a,b platí:

• 
• 
• 
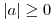
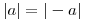
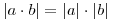
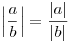• , pokud b ≠ 0
  
  

Někde se také uvádí, že absolutní hodnota reálného čísla udává jeho vzdálenost jeho obrazu na číselné ose od počátku (od obrazu nuly). Takže třeba |−3| = |3|, protože obě čísla jsou stejně daleko od počátku (od nuly), jen každé leží na opačné straně. Zápis |a − b| pak můžeme interpretovat jako vzdálenost obrazu čísla a od obrazu čísla b. Samozřejmě, že je jedno, jestli měříme vzdálenost a od b, nebo b od a. Platí tedy: |a − b| = |b − a|.

Jednoduché rovnice a nerovnice

Příklad 1

Řešte v 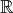dané rovnice a nerovnice zpaměti :

Následující rce a nerce jsou velmi jednoduché, proto si tentokrát odpustíme určování O a D u každého příkladu zvlášť. Ve všech případech bude totiž stejně platit, že .

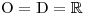|x| = 2,5

Ve všech příkladech zde řešených budeme absolutní hodnotu interpretovat jako nějakou vzdálenost obrazů dvou čísel na číselné ose.

Zadanou rovnici tedy můžeme "přečíst" takto: Hledáme taková reálná čísla x, aby jejich vzdálenost od počátku byla 2,5. Načrtneme si číselnou osu, vyznačíme si počátek a určíme všechna čísla, jejichž obrazy jsou o něj vzdáleny 2,5.

Nikoho by nemělo překvapit, že to budou právě dvě čísla, a to −2,5 a 2,5.

Tedy K = {−2,5; 2,5}.

|x − 2| = 3

Podle výše uvedených poznámek můžeme výraz |x − 2| "přečíst" jako: Vzdálenost čísla x od 2.

Hledáme tedy taková čísla, jejichž obrazy na číselné ose mají vzdálenost 3 od obrazu čísla 2.

Při pohledu na číselnou osu pak snadno určíme, že to jsou právě čísla 5 a také −1.

K = {−1; 5}.

|x + 1| = 4

Abychom opět interpretovali absolutní hodnotu na levé straně rovnice, musíme si ji upravit. Chceme-li ji totiž chápat jako vzdálenost dvou "čísel", musí být v absolutní hodnotě znaménko mínus, nikoliv plus.

Výraz na levé straně tedy upravíme takto: |x − (−1)|.Pokud takto upravujeme výraz v abs. hodn., je vhodné nechat kladné znaménko u neznámé a vytvořit záporné u čísla.

Teď už není problém zjistit, že dvě čísla, jejichž obrazy mají od obrazu −1 vzdálenost 4, jsou −5 a 3.

K = {−5; 3}.

|2 + x| ≤ 3

Nerovnice nebude v tomto případě od rovnic příliš odlišovat, jen si musíme uvědomit, že nerovnici v oboru reálných čísel zpravidla řeší nekonečně mnoho čísel.

Nejprve si upravíme výraz v absolutní hodnotě: |2 + x| = |−(−2) + x | = | x − (−2)|.

Interpretace této nerovnice bude znít takto: Hledáme čísla x taková, aby vzdálenost jejich obrazů na číselné ose od obrazu čísla −2 byla menší nebo rovna 3.

Načrtneme si číselnou osu, vyznačíme počátek a číslo −2, na každou stranu vyznačíme vzdálenost 3. Pak všechna čísla, která leží uvnitř tohoto vymezeného intervalu, mají vzdálenost od −2 menší nebo rovnu 3.

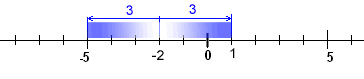
Kořeny této nerovnice tedy budou všechna reálná čísla mezi −5 a 1, včetně těchto "hraničních" čísel.

K = <−5; 1>.

Jednoduché rovnice a nerovnice s neznámou v absolutní hodnotě se samozřejmě dají řešit i jinak,
ale výše uvedená metoda je nejrychlejší a poměrně názorná. Ostatně i v jiných
partiích matematiky se absolutní hodnota používá k vyjádření vzdálenosti.
Třeba v geometrii znamená zápis|AB| vzdálenost bodů A a B.

Takto jednoduše se dají řešit pouze rovnice a nerovnice, které obsahují jen jednu absolutní hodnotu, ve které je pouze lineární dvojčlen a mimo absolutní hodnotu je jen jedno číslo. Pokud toto není splněno, budeme rovnice a nerovnice řešit pomocí tabulky obdobně jako u lineárních nerovnic v podílovém tvaru.

Řešení pomocí tabulky

Řešení si vysvětlíme rovnou na příkladu jedné rovnice s dvěma absolutními hodnotami, které obsahují neznámou.

Příklad 1

Řešte v 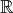rovnici .

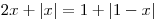Nejprve určíme O a D. Absolutní hodnota je definována pro jakékoliv reálné číslo, bude to i tentokrát spíše formalita:

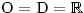
Obdobné příklady se vždy řeší tak, že se snažíme nahradit výrazy s absolutní hodnotou nějakými ekvivalentními bez absolutní hodnoty, a to za jistých podmínek. Z definice absolutní hodnoty víme, že máme-li v absolutní hodnotě nezáporný výraz, můžeme absolutní hodnotu klidně odstranit a výraz bude mít stejnou hodnotu. Pokud je uvnitř záporný výraz, stačí celou absolutní hodnotu nahradit opačným výrazem k "vnitřku". Ukážeme si to na příkladu absolutní hodnoty |1 − x| ze zadané rovnice.

Pro x ≤ 1 je výraz v absolutní hodnotě |1 − x| nezáporný a podle definice absolutní hodnoty můžeme nahradit výrazem 1 − x.

Podobně pro x > 1 je "vnitřek" absolutní hodnoty |1 − x| záporný a můžeme ji nahradit výrazem − (1 − x), neboli x − 1.

Řešení rovnice bychom tedy rozdělili do dvou větví: pro x ≤ 1 a pro x > 1. Zadaná rovnice ale obsahuje ještě jednu absolutní hodnotu, a proto bychom museli každou z těchto dvou větví dělit ještě na další dvě, abychom mohli nahradit i tu druhou absolutní hodnotu. V případě 3 absolutních hodnot s neznámou v zadání by pak došlo na rozdělení
do 8 větví výpočtu, při 4 absolutních hodnotách k 16 větvím apod.

Proto bude lepší řešit obdobné rovnice a nerovnice pomocí tabulky.

---

Nejprve určíme nulové body výrazů uvnitř všech absolutních hodnot. Tato čísla jsou velmi důležitá, neboť vymezují, pro která reálná čísla bude "vnitřek" absolutních hodnot kladný a pro která bude záporný. Pozor, bude-li absolutní hodnota obsahovat kvadratický výraz,
může mít "vnitřek" nula až dva nulové body.

Daná rovnice 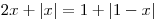má nulové body x₀₁ = 0 a x₀₂ = 1.

Nyní vytvoříme tabulku:

První řádek pak bude reprezentovat číselnou osu, kterou rozdělíme na jednotlivé úseky podle nulových bodů. Oproti tabulkám při řešení nerovnic v podílovém tvaru nemusíme jednotlivé nulové body řadit do zvláštních sloupečků. Dokonce ani nemusíme přemýšlet, do kterého sloupečku je zařadit, klidně je zařadíme do obou. Tato čísla totiž
reprezentují stav, kdy je "vnitřek" absolutní hodnoty nulový. Je pak jedno, jestli |0| nahradíme 0, nebo −0. Do buněk prvního sloupečku od druhého řádku pak zapíšeme jednotlivé výrazy s neznámou v absolutní hodnotě, které chceme nahrazovat.

V tomto konkrétním příkladě tedy dostaneme:

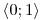
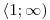
|x|
|1 − x|

Nyní začneme tabulku vyplňovat. Sloupce tabulky nám vymezily intervaly, na kterých budeme řešit ekvivalentní rovnice s rovnicí ze zadání. V těchto sloupcích nahradíme postupně všechny výrazy s absolutní hodnotou ekvivalentními výrazy bez absolutních hodnot. Určíme, jakého znaménka je "vnitřek" každé absolutní hodnoty pokud neznámá může nabývat jen hodnot z daného intervalu.
Absolutní hodnotu pak nahradíme nezměněným výrazem z "vnitřku" v případě, že znaménko bylo +,
nebo opačným výrazem z "vnitřku" v případě, že znaménko bylo −.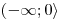

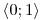
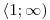
|x|	− (−x)	+ (x)	+ (x)
|1 − x|	+ (1 − x)	+ (1 − x)	− −(1 − x) = (x − 1)
V následujícím řádku tabulky pak vyřešíme na příslušném intervalu daným sloupcem (novém oboru řešitelnosti O) rovnice, po nahrazení absolutních hodnot.
	O1 = D1 =	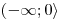O2 = D2 =	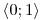O3 = D3 =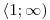
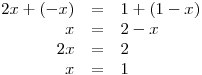
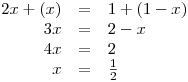
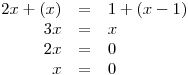
	Určili jsme, že x = 1, ale tato hodnota neleží v D1, a tedy K1 = ∅.	Vypočtená hodnota tentokrát leží v D2, a tedy 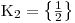.	Stejně jako v prvním sloupci i vypočetené číslo 0 neleží v D3, a tedy K3 = ∅

Výsledné K určíme jako sjednocení K₁ ∪ K₂ ∪ K₃.

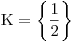
Řešení rovnice se hodně protáhlo díky velkému vysvětlování postupu.
U dalších rovnic budeme postupovat už rychleji.

Obdobně se pak řeší i nerovnice s neznámou v absolutní hodnotě.

Příklad 2

Řešte v 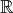nerovnici .

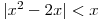Řešení

Určíme nulové body výrazu v absolutní hodnotě: x₀₁ = 0, x₀₂ = 2.

Sestavíme a vyplníme tabulku:

	+	−	+
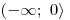
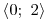
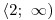
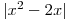
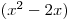
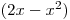
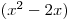
Vyřešíme kvadratické nerovnice v jednotlivých sloupečcích grafickou metodou. Všimněte si, že nerovnice v 1. a 3. sloupečku vypadají stejně, jen se řeší v jiném intervalu. Nerovnici tedy stačí upravíme jen jednou, ale řešení určíme pro každou zvlášť.
	O1 = D1 =	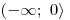O2 = D2 =	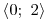O3 = D3 =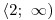
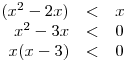
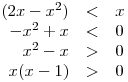
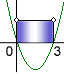
	x1 = 0, x2 = 3	x1 = 0, x2 = 1
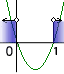
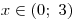
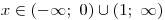
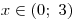
Nezapomene určit průnik vypočteného řešení jednotlivých sloupečků s určenými D1, D2, D3. Teprve pak dostaneme K1, K2, K3.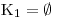

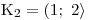
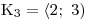
Zbývá už jen určit výsledné K jako sjednocení K₁ ∪ K₂ ∪ K₃.

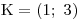
Důležité u podobných příkladů je nezmatkovat v tabulce, určit si pro každý sloupeček
příslušné O a D a vypočtené množiny kořenů s nimi VŽDY proniknout!
Určená K se pak už jednoduše sjednotí do výsledného.

<<iracionální rovnice a nerovnice – úlohy rovnice s parametry>>

úvod : lineární rce : lineární nerce : kvadratické rce : kvadratické nerce : iracionální rce a nerce : rce s abs. hodnotou a parametry : rce vyšších řádů : soustavy : odkazy

Copyright (c) 2008 Jaromír Gloc. Všechna práva vyhrazena.