ROVNICE
A NEROVNICE

Úvod Lineární rovnice Lineární nerovnice  Test 1 – lineární Kvadratické rovnice Kvadratické nerovnice  Test 2 – kvadratické Iracionální rce a nerce Parametry a abs. hodn. Rovnice vyšších řádů Kubická rovnice Speciální rce vyšších řádů  Test 3 Soustavy rovnic  Test 4 – soustavy Odkazy a literatura
Přehled stránek

Bikvadratické rovnice

Bikvadratickou rovnicí

nazveme každou rovnici, která se dá ekvivalentními úpravami převést na tvar ax⁴ + bx² + c = 0, kde x je neznámá, koeficienty a, b, c 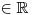a a ≠ 0.

Bikvadratické rovnice se řeší pomocí substituce, kdy původní výraz s neznámou x celý nahradíme novou neznámou, např. y. V případě bikvadratických rovnic každý výskyt x² v zadání rovnice nahradíme y.

Rovnici z definice pomocí substituce upravíme takto:

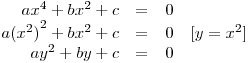
Tím jsme dostali kvadratickou rovnici s neznámou y, kterou už umíme snadno vyřešit. Pokud nám vyjdou dva kořeny y₁ a y₂, nesmíme zapomenout, že původní rovnici řešíme pro x a y = x². Musíme proto ještě vyřešit dvě rovnice x² = y₁ a x² = y₂. Pak teprve získáme všechny kořeny původní bikvadratické rovnice ax⁴ + bx² + c = 0 s neznámou x.

Pokud by rovnice se substituovanou neznámou y neměla kořeny, pak nebude mít kořeny ani rovnice původní. Má-li kořeny rovnice s neznámou y, neznamená to ještě, že bude mít kořeny i původní rovnice.

Příklad 1

Řešte v 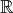rovnici .

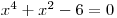Řešení

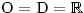
Zavedeme substituci s = x² a rovnici převedeme do tvaru:

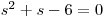
Tu vyřešíme pomocí vzorečku s diskriminantem.

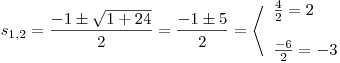
Vyšly nám kořeny 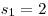a 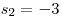. Nyní je čas odstranit substituci .

Neboli vyřešíme rovnice 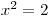a .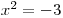

První má kořeny 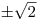a druhá žádné reálné kořeny nemá. Pokud to nevidíte rovnou, vyřešte si obě rce třeba vzorečkem s diskriminantem.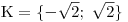

Nikdy nesmíte zapomenout na konci podobných příkladů provést odstranění substituce, tj. vrátit
se zpět k původní proměnné.

Obdobně se dají řešit trinomické rovnice, jejichž základní tvar je . V nich zavádíme substituci y = xⁿ, vyřešíme kvadratickou rovnici pro y a odstraníme substituci. Při odstraňování substituce totiž budeme řešit binomické rovnice.

Binomické rovnice

Binomické rovnice jsou rovnice ve tvaru xⁿ = k, kde x je neznámá, k je libovolné reálné (častěji spíše komplexní) číslo a n je přirozený exponent.

Binomické rovnice se nejčastěji řeší v oboru komplexních čísel a pečlivě se jim věnuje diplomová práce Lenky Svobodové (Šilarové), proto se jim v této práci věnovat nebudeme.

Reciproké rovnice

Reciproká rovnice n-tého stupně

je každá rovnice, která se dá upravit na tvar

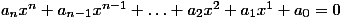
kde a_n ≠ 0 a pro jejíž koeficienty a_k; k = 0, 1,..., n-1, n platí:

• a_k = a_n−k ,  pak rovnici nazveme reciprokou rovnicí I. druhu. (kladně reciprokou rovnicí).
• a_k = −a_n−k , pak rovnici nazveme reciprokou rovnicí II. druhu (záporně reciprokou rovnicí, někdy též antireciprokou).

Přirozené číslo n nazveme stupeň reciproké rovnice.

Příklady

−5x³ + 2x² + 2x − 5 = 0 je reciproká rovnice I. druhu 3. stupně.

2x⁴ −x³ − 3x² − x + 2 = 0 je reciproká rovnice I. druhu 4. stupně.

−4x⁴ + 2x³ − 2x + 4 = 0 je reciproká rovnice II. druhu 4. stupně. Reciproká rovnice II. druhu sudého stupně musí mít prostřední člen s koeficientem 0.
To je totiž jediné číslo, které může splnit podmínku z definice.

Hodnoty koeficientů jsou symetrické (až na znaménko u II. druhu) podle "prostředku" výrazu
na levé straně rce. To je buď prostřední člen u rovnic sudého stupně,
nebo je mezi dvěma prostředními výrazy u rovnic lichého stupně.

Každá reciproká rovnice obsahuje nenulový absolutní člen, proto nemají reciproké rovnice kořen 0. Má-li reciproká rovnice kořen , pak má za kořen i číslo . Číslo se totiž někdy nazývá

reciprokým číslem k číslu x₁.

Postup řešení reciproké rovnice I. druhu

Reciproké rovnice sudého stupně (n=2m; m ∈ ).

1. Vydělíme obě strany rovnice výrazem x^m
2. Z prvního a posledního členu, druhého a předposledního apod. vytkneme jejich koeficient. Protože máme reciprokou rovnici I. druhu sudého stupně, budou oba koeficienty stejné.
3. V rovnici zavedeme substituci .

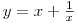Dostaneme obecnou rovnici m-tého stupně s neznámou y, kterou ale nemusí být jednoduché vyřešit.

Reciproké rovnice lichého stupně (n=2m + 1; m ∈ ).

Tyto rovnice mají vždy kořen −1. Toto snadno ověříme dosazením. Ten si zapíšeme a rovnici vydělíme výrazem x + 1. Dostaneme reciprokou rovnici I. druhu sudého stupně 2m.

Příklad 2

Řešte v 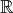rovnici −5x³ + 2x² + 2x − 5 = 0.

Řešení

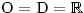
Máme zadanou reciprokou rovnici I. druhu lichého stupně. Ta má vždy kořen −1. Ten si zapíšeme a rovnici vydělíme výrazem x + 1. To sice není ekvivalentní úprava, ale můžeme si ji
dovolit, protože jsme si už jeden kořen (−1) určili.
Výsledná rce po dělení nebude mít stejné K jako rce
původní, ale množiny všech kořenů obou rovnic
se budou lišit jen o kořen −1.

Dostáváme rovnici −5x² + 7x − 5 = 0. To je sice reciproká rovnice I. druhu sudého stupně, ale také je to kvadratické rovnice, jejíž kořeny lze určit třeba vzorečkem s diskriminantem.

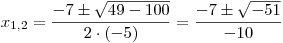
Vyšel nám diskriminant kvadratické rovnice záporný, proto nebude mít reciproká rovnice ze zadání už žádné jiné reálné kořeny, kromě prvně nalezené −1.

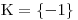
Ačkoliv jsme tuto rci řešili postupem pro rce reciproké, uvědomte si, že to je kubická rce.
Jak je vidět, tato má pouze jeden povinný reálný kořen,
na který bychom mohli přijít i pokusným dosazováním.

Postup řešení reciproké rovnice II. druhu

Tyto rovnice mají vždy kořen 1; Opět lze snadno ověřit dosazením. dělíme ji tedy výrazem x − 1 (kořen 1 si zapamatujeme), a vždy získáme reciprokou rovnici I. druhu sudého stupně.

Příklad 3

Řešte v rovnici −5x⁵ + 2x⁴ + x³ − x² − 2x + 5 = 0.

Řešení

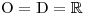
V zadání máme reciprokou rovnici II. druhu, která má vždy kořen 1. Zapamatujeme si tedy tento kořen a obě strany rovnice vydělíme výrazem x − 1.

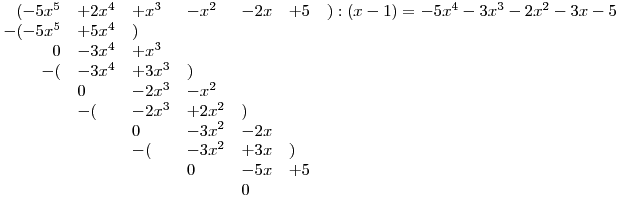
Převedli jsme řešení reciproké rovnice ze zadání na řešení reciproké rovnice I. druhu:

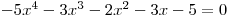
Vydělíme tedy obě strany rovnice výrazem x² a upravíme na tvar vhodný pro substituci.

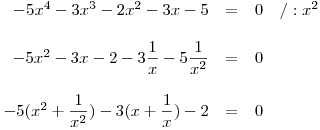
Zavedeme substituci 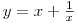, přičemž 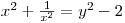, a rovnici upravíme.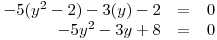

Vypočteme kořeny y_1,2:

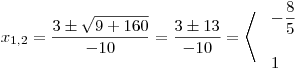
Teď je třeba odstranit substituci v rovnici a z vypočtených kořenů y získat kořeny x.

Budeme tedy řešit tyto dvě rovnice:

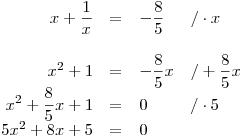
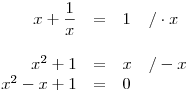
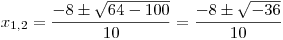
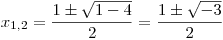
V obou případech se ale dostaneme k záporným diskriminantům a tudíž neexistují reálné kořeny, které by řešily rovnici .

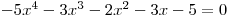Reciproká rovnice ze zadání pak má jen jeden reálný kořen a to 1, na který jsme přišli hned na začátku.

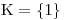
Nakonec by se dalo říci, že jsme celý výpočet dělali zbytečně, protože nám neposkytl žádné
další kořeny, o kterých bychom nevěděli hned na začátku. Ale není to pravda. Zjistili jsme,
že tato rovnice má jistě jen jeden reálný kořen a kdybychom chtěli celou rovnici řešit
v komplexním oboru, snadno bychom teď dopočítali zbylé 4 komplexní kořeny.

V běžné školské praxi se řeší reciproké rovnice obou druhů maximálně pátého stupně, protože po všech úpravách a substitucích z nich dostaneme řešení kvadratické rovnice, kterou umíme vyřešit vždy a efektivně. Kdybychom ale stupeň reciproké rovnice navýšili jen třeba na šest, dostali bychom po substituci kubickou rovnici, jejíž řešení nemusí být vůbec jednoduché.

Více se reciprokým rovnicím věnují v Polák [8] nebo v Kotulková [5]. V první jmenované publikaci pak najdete i důkazy zde používaných tvrzení.

<<kubické rovnice Test na iracionální, parametrické, a další speciální rovnice>>

úvod : lineární rce : lineární nerce : kvadratické rce : kvadratické nerce : iracionální rce a nerce : rce s abs. hodnotou a parametry : rce vyšších řádů : soustavy : odkazy

Copyright (c) 2008 Jaromír Gloc. Všechna práva vyhrazena.