Úlohy k opakování
-
Úloha 1
Řešte v
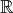 rovnici
rovnici 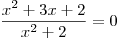 .
. -
 Určíme O a D.
Určíme O a D.
Pro určení definičního oboru D vyřešíme pomocnou rci
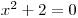 .
.Diskriminant
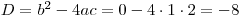 , proto pomocná rce nemá žádný reálný kořen. Tedy jmenovatel zlomku na levé straně rovnice nikdy nenabývá nulové hodnoty.
, proto pomocná rce nemá žádný reálný kořen. Tedy jmenovatel zlomku na levé straně rovnice nikdy nenabývá nulové hodnoty.
 Upravíme danou rci na základní tvar.
Upravíme danou rci na základní tvar.
Jmenovatel je pro každé reálné x nenulový, proto jím můžeme vynásobit obě strany rovnice:
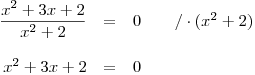
 Vypočteme pomocí vzorečku kořeny.
Vypočteme pomocí vzorečku kořeny.
Určíme kořeny poslední rce:
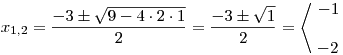
 Určíme K.
Určíme K.
Zapíšeme
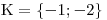 .
. Nekomplikované řešení rce, které zpestřil jen jmenovatel zlomku v zadání,
Nekomplikované řešení rce, které zpestřil jen jmenovatel zlomku v zadání,
který ač obsahuje neznámou x, tak nikdy není nulový a proto platí O = D.

-
Úloha 2
Zjednodušte daný výraz a určete, pro která x má smysl.
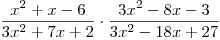
-
 Vypočteme kořeny kvadratické rce příslušné k trojčlenu v čitateli prvního zlomku.
Vypočteme kořeny kvadratické rce příslušné k trojčlenu v čitateli prvního zlomku.
Vypočteme kořeny rce:
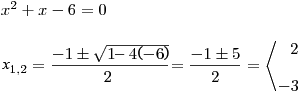
 Někdy se vyplatí pro určení kořenů vhodně použít Vietovy vzorce. Dosadíme-li do vzorečků
Někdy se vyplatí pro určení kořenů vhodně použít Vietovy vzorce. Dosadíme-li do vzorečků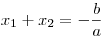 a
a 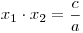 , vyjde nám x1 + x2 = −1 a x1⋅ x2 = 6. Z těchto dvou rovnic je pak
, vyjde nám x1 + x2 = −1 a x1⋅ x2 = 6. Z těchto dvou rovnic je pak
snadné určit, že kořeny budou 2 a −3. Vypočteme kořeny kvadratické rce příslušné k trojčlenu ve jmenovateli prvního zlomku.
Vypočteme kořeny kvadratické rce příslušné k trojčlenu ve jmenovateli prvního zlomku.
Vypočteme kořeny rce:
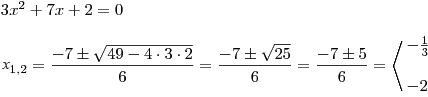
 Vypočteme kořeny kvadratické rce příslušné k trojčlenu v čitateli druhého zlomku.
Vypočteme kořeny kvadratické rce příslušné k trojčlenu v čitateli druhého zlomku.
Vypočteme kořeny rce:
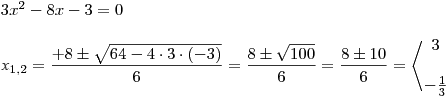
 Vypočteme kořeny kvadratické rce příslušné k trojčlenu ve jmenovateli druhého zlomku.
Vypočteme kořeny kvadratické rce příslušné k trojčlenu ve jmenovateli druhého zlomku.
Vypočteme kořeny rce:
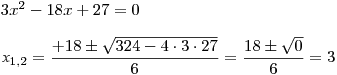
 Přepíšeme kvadratické trojčleny v zadání jako součiny lineárních dvojčlenů.
Přepíšeme kvadratické trojčleny v zadání jako součiny lineárních dvojčlenů.
Rozložíme kvadratické trojčleny na součiny lineárních dvojčlenů.
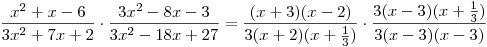
 Výrazy zkrátíme.
Výrazy zkrátíme.
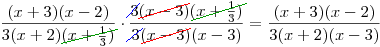
 Určíme podmínky platnosti.
Určíme podmínky platnosti.
Zakážeme, aby x nabývalo hodnot nulových bodů všech lineárních dvojčlenů, které se nám objevily ve jmenovateli.
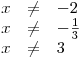
 Toto byl další z postupově nekomplikovaných příkladů, který kromě základních znalostí rozkladu
Toto byl další z postupově nekomplikovaných příkladů, který kromě základních znalostí rozkladu
kvadratických trojčlenů, vyžaduje jen dostatečnou pozornost a pečlivost při řešení, abychom
neudělali numerické chyby.

Testíky
Klikněte na otazník u odpovědi, o které myslíte, že je dobře, a smajlík vám prozradí, zda jste odpověděli správně. U každého příkladu je jen jedna správná možnost.
|
Rovnice 4x2 = 4 je ekvivalentní s rovnicí:
|
Určete K pro rovnici x2 = 36, za předpokladu, že O = D =
|
|
Určete K pro rovnici x2 + 4= 0.
|
Určete K pro rovnici x2 + 2x + 1= 0.
|
Řešení dalších úloh si můžete vyzkoušet v testu v kapitole za kvadratickými rovnicemi a nerovnicemi.

 (2x − 2)2 = 0
(2x − 2)2 = 0